The study titled “Effect of sojourn time distributions on the early Dynamics of COVID-19 outbreak” led by ITU Department of Mathematics member Prof. Dr. Murat Sarı was published in Nonlinear Dynamics.
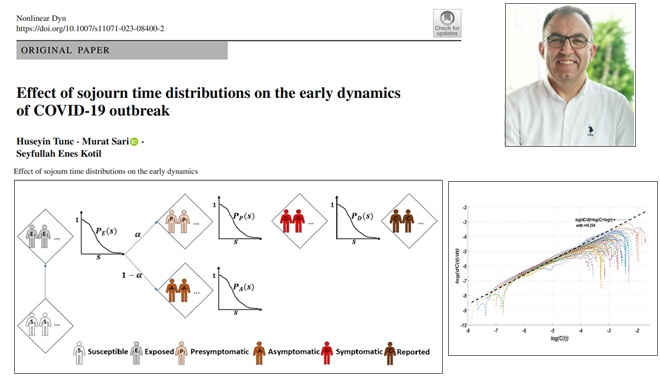
This study proposes a new model for investigating infectious diseases, specifically the COVID-19 outbreak. The SEPADC model allows for arbitrarily distributed latency and infectiousness periods and is represented by nonlinear Volterra integral equations. The study aims to derive a general relationship between the intrinsic growth rate and the basic reproduction number using the Lotka-Euler equation. The study finds that the exponential distribution assumption of sojourn times has led to the underestimation of R0 values for most countries and that R0 estimates are affected by the choice of sojourn time distributions. The study estimates R0 values for 152 countries using the new model and finds a global convergence of R0 = 4.58. The study also shows that increasing the shape parameter of the Erlang distributed sojourn times increases the skewness of the epidemic curves.
https://link.springer.com/article/10.1007/s11071-023-08400-2